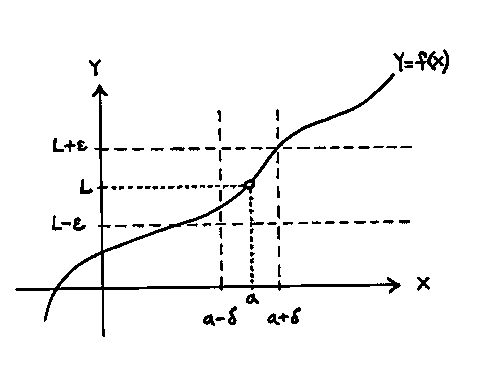
Basic Calculus Problems: Definition Of A Limit
The definition of a limit continues on in our learning limits and how they are applied. Specifically we are going to look at some proofs in this section. With a precise definition we can now prove many limit properties.
Definition of a Limit

The \(\delta\) value will always depend on the \(\epsilon\) value. That is important to remember in order to understand what is happening in these limits. Once you find a value that works in your problem then smaller values of that \(\delta\) also work.
Problem 1.
For the given function f(x) and values L,c, and \(\epsilon\) > 0 find the largest open interval about c on which the inequality |f(x)-L| < \(\epsilon\) holds. Then determine the largest value for \(\delta\) >0 such that 0<|x-c|<\(\delta\)\(\rightarrow\) |f(x)-L|<\(\epsilon\).
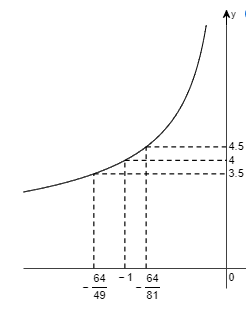
f(x) = \(\frac{1}{x}\), L= 0.125, c = 8, \(\epsilon\) = 0.015
Solve |f(x) - L| < \(\epsilon\) to find the largest interval containing c on which the inequality holds.
Write the inequality without absolute value. Substitute \(\frac{1}{x}\) for f(x), 0.1215 for L, and 0.015 for \(\epsilon\).
|f(x)-L| < \(\epsilon\)
|\(\frac{1}{x}\) - 0.125| < 0.015
-0.015 < \(\frac{1}{x}\) - 0.125 < 0.015
Simplify by adding 0.125 to all expressions.
-0.015 < \(\frac{1}{x}\) - 0.125 < 0.015
0.11 < \(\frac{1}{x}\) < 0.14
Simplify further by taking the reciprocals of all terms. Be sure to reverse the inequalities. Make sure you check that the rounded endpoints still allow the inequality |f(x)-L| < \(\epsilon\) to hold true.
9.0909 > x > 7.1429
Since the interval 7.1429 < x < 9.0909 is not centered on c=8, \(\delta\) is the distance from 8 to closer endpoint of the interval. The value of \(\delta\) is then 0.8571.
Problem 2.
For the given function \(f(x)\), the point \(c\), and a positive number \(\epsilon\), find \(L=lim f(x)\). Then find a number \(\delta\) > 0 such that for all x, 0<|x-c|<\(\delta\)\(\rightarrow\)|\(f(x)-L\)| < \(\epsilon\).
\(f(x)=8-3x, c=4, \epsilon=0.03\)
Notice that \(f(x)\) is a linear function. Since a linear function is a simple polynomial function and it is defined for all \(x\), the limit \(L\) = lim is the value of \(f(x)\) at \(c\).
Evaluate the function at \(c=4\).
\(L=8-3(4)=-4\)
To find \(\delta\), begin by solving the inequality \(|f(x)-L|<\epsilon\) to find an open interval \((a,b)\) containing \(c\) on which the inequality holds for all \(x\neq c\).
Remove the absolute value sign and rewrite the inequality as a compound inequality.
\(|(8-3x)-(-4)| < 0.03\)
\(-0.03 < (8-3x) - (-4) < 0.03\)
Simplify the center expression and isolate the x-term.
\(-0.03 < -3x+12 < 0.03\)
\(-12.03 < -3x < -11.97\)
Then isolate \(x\) in the center. Notice that the direction of the inequalities has been changed.
\(4.01 > x > 3.99\)
Therefore, for \(x\) in the interval \((3.99,4.01)\), the inequality \((8-3x)-(-4)|<0.03\) holds. Now choose a positive value for \(\delta\) that places the open interval \((c-\delta,c+\delta)\) centered on \(c\) inside the interval \((3.99,4.01)\).
The distance to the first endpoint is \(4-3.99=0.01\).
The distance to the second endpoint is \(4.01 -4=0.01\).
The largest possible value for \(\delta\) is \( 0.01\).
Therefore, for all \(x\) satisfying \(0<|x-4|<0.01\), the inequality \(|(8-3x)-(-4)|<0.03\) holds.
Problem 3.
Give an \(\epsilon - \delta\) proof of the limit fact.
\(lim_{x \to 0}(5x+1)=1\)
We begin by giving the precise meaning of a limit.
To say that \(lim f(x)=L\) means that for each \(\epsilon>0\) there is a corresponding \(\delta>0\) such that \(|f(x)-L|<\epsilon\), provided that \(0<|x-c|<\delta\).
To establish the proof, we first perform a preliminary analysis to find the appropriate choice of \(\delta\).
Let \(\epsilon\) be any positive number.
We must produce a \(\delta > 0\) such that \( 0<|x-0|<\delta \rightarrow |(5x+1) -1 < \epsilon\).
By simplifying the inequality on the right, we will determine the value of \(\delta\) needed for the inequality on the left.
\(|(5x+1)-1| < \epsilon \Leftrightarrow |5x| < \epsilon \)
\(\Leftrightarrow |5| |x| < \epsilon\)
\(\Leftrightarrow 5|x| < \epsilon\)
\(\Leftrightarrow |x| < \frac{\epsilon}{5}\).
Now we see that we should choose \(\delta=\frac{\epsilon}{5}\). We can now construct the formal proof of the statement \(\lim_{x \to 0}(5x+1)=1\).
Let \(\epsilon > 0\) be given. Choose \(\delta=\frac{\epsilon}{5}\). Then \(0<|x-0|<\delta\) implies the following chain of equalities and an inequality.
\(|(5x+1)-1| = |5x|\) Simplify inside the absolute value bars.
\( = |5| |x|\) Rewrite as product of absolute values.
\( = 5 |x| \) Simplify.
\( =5 |x-0|\) Rewrite expression inside absolute value bars.
\( < 5\delta\) Apply the condition \(0<|x-0|<\delta\).
\( = \epsilon \) Substitute \(\delta=\frac{\epsilon}{5}\).
The result of the above chain of equalities and an inequality is that \(|(5x+1)-1|< \epsilon\).
Therefore, we have proven that \(\lim_{x \to 0}(5x+1)=1\).
Conclusion
The definition of a limit has some nice proofs that can establish. If you go over these problems slowly the ideas behind limits will begin to emerge. While this section is short it is essential to understanding limits and beginning calculus in general.