One-Sided Limits Of Calculus
In a continuance of this series today, I wanted to talk about the one-sided limits of calculus. Limits and where they lead are one of the fundamental concepts of calculus. Since limits show what happens near any particular point on a graph we need to take a look at them. Read on with me and I will explain their behavior so you can easily solve them.
One-Sided Limits
Our current idea of the limit definition goes back around 200 years ago by Bernard Bolzano. He was instrumental in several mathematical ideas. One of which was the definition of one-sided limits which I will be talking about today. Now on to some problems!
Problem 1.
Use the graph to see if the following statements are true or false. Look at the graph carefully because it can be tricky to see what is really going on sometimes.
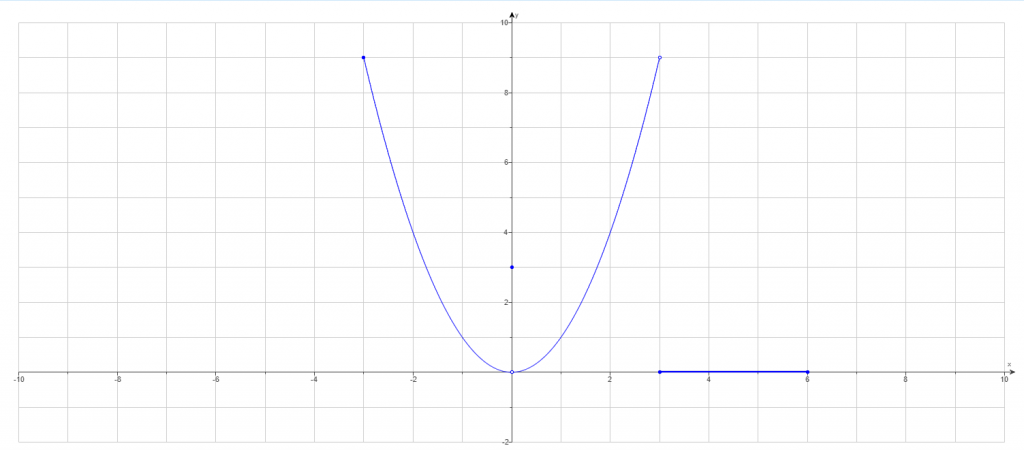
We can see there is a function \(y=f(x)\). There is also a small portion of the positive x-axis defined from [3 to 6].
A. True or False: \(lim_{x \to -3+}(f(x)=9\)
F(x) is your [y] value. X is of course your [x] value. Does [y] or [f(x)] get closer to 9 as [x] gets closer to 3 when coming from larger numbers than +3 ?
We can see that it sure does. The answer is [true].
B. True or False: \(lim_{x \to 0-}(f(x)=3\)
F(x) is your [y] value. X is your [x] value. The question is asking if [y=3] as [x] approaches 0 from the negative side of the [x] axis ?
It appears that [y=0] when [x=0] so the answer is false for this question.
C. True or False: \(lim_{x \to 0-}(f(x)\) = \(lim_{x \to 0+}(f(x)\) ?
This question is asking if the left limit is the same as the right limit. What does [y] equal when [x] is coming from the negative side? It equals 0. Now what does [y] equal as [x] is coming from the positive side? It equals 0 also. So both one-sides limits equal each other and the answer to the question is [true].
D. True or False: \(lim_{x \to 0}(f(x)\) exists?
We have basically answered this question already. When the limit is listed without directional signs(- or +) it is asking if the limit exists and is equal from both sides of the graph. It is equivalent to asking if the limit from the left side equal the limit from the right side? As mentioned before we have answered this. We did see that the limit from the left side equaled the limit from the right side. So the answer to this question is [true].
E. True or False: \(lim_{x \to 0}(f(x)=0\)
This is another version of the question above. Since there are no directional signs(- or +) it is implying the full limit. The full limit is each one-sided limit being equal to each other. The left hand limit=0. The right hand limit=0. Therefore the limits equal each other and both equal 0. So the answer is also true for this question.
F. True or False: \(lim_{x \to 3}(f(x)=9\)
F(x) is your [y] value. X is your [x] value. The question is asking if [y=9] whether [x] approaches 3 from the negative or positive side?
When [x] is coming from the positive side of the [x] axis things are pretty clear and defined. However, there is a hole in the graph when [x] approaches 3 from the negative side. Therefore our limits are not equal and the answer is [false].
G. True or False: \(lim_{x \to 6-}(f(x)=6\)
F(x) is your [y] value. X is your [x] value. This is asking if [y=6] when [x] approaches 6 from the negative side? We can plainly see that it does not. When [y=6] it looks like [x] is somewhere between 2 and 3. So the answer to this question is [false].
Problem 2.
F(x) = 6-x when x < 2 and (x/2) +1 when x > 2.
Find \(lim_{x \to 2+}(f(x)\) and \(lim_{x \to 2-}(f(x)\).
This is what I call a conditional function. Certain sections of the function give different values depending on the condition.
We will start by looking at the one-sided limits. First lets look at the limit as [x] approaches 2 from the positive side of the x-axis. The expresison (x/2) + 1 is used to evaluate when x > 2.
The \(lim_{x \to 2+}(f(x)=((x/2)+1)\) = (2/2) + 1 = 2.
The expression 6-x is used to evaluate the expression when x < 2.
The \(lim_{x \to 2-}(f(x)=6-x\) = 6-2 = 4.
Does the limit exist? For a full limit to exist its one-sided limits have to exist and be equal. The two limits above that we evaluated are not equal. Therefore the limit does not exist.
Problem 3.
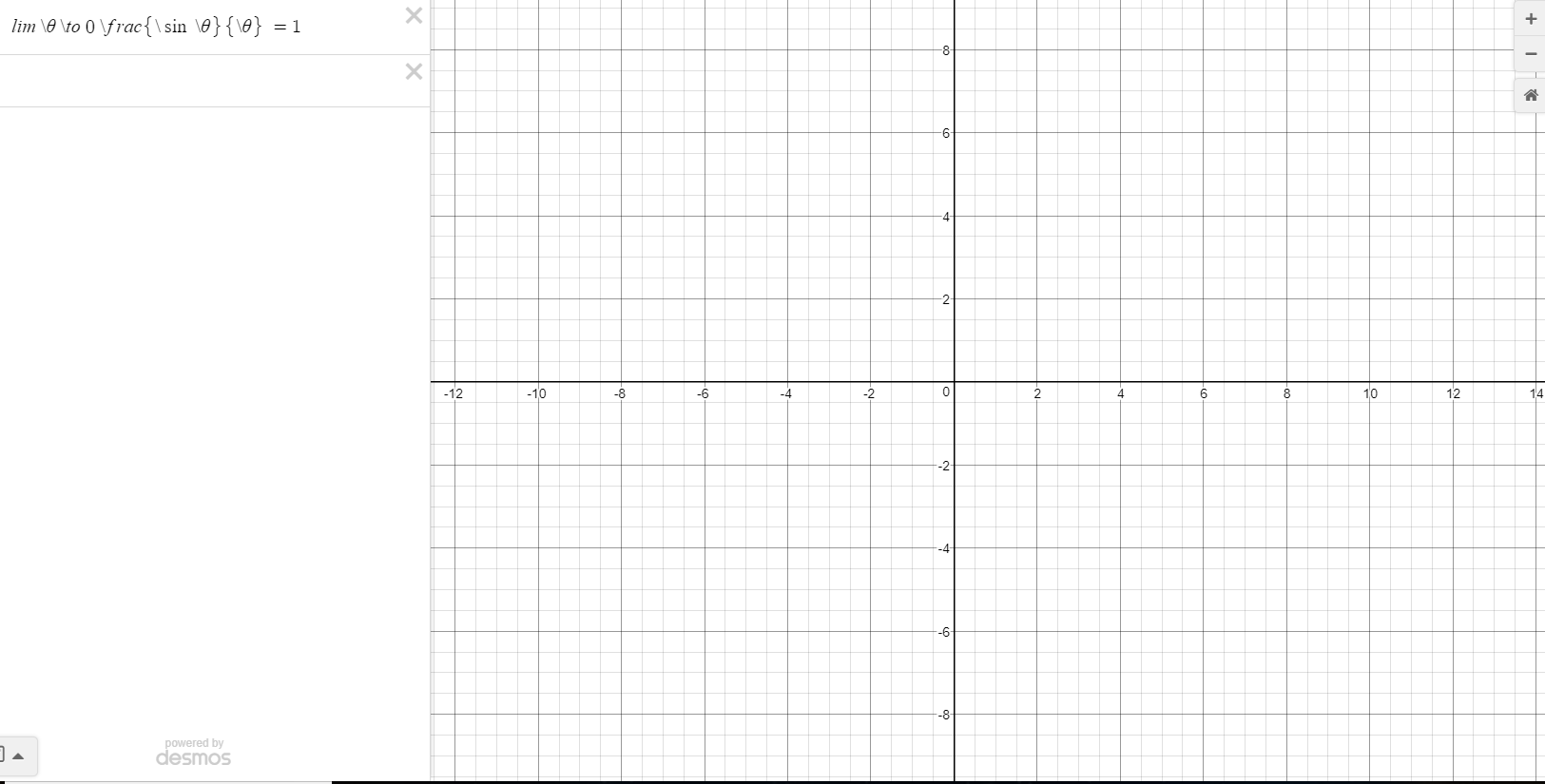
Use the relation \(lim_{\theta \to 0}{\frac{\sin\theta}{\theta}}=1\) to find the limit of this function.
\(\frac{\sin \sqrt{2} \theta}{\sqrt{2} \theta}\)
As \(\theta\) gets closer to 0 the square root of \(\theta\) also gets closer to 0.
We now have : \(lim_{\sqrt{2}\theta \to 0}{\frac{\sin \sqrt{2} \theta}{\sqrt{2} \theta}}\)
So \(x = \sqrt{2} \theta \). Now substitute in the values.
\(lim_{x \to 0} \frac{\sin x}{x} =1 \). That is our answer using the relation.
Problem 4.
Find the limit of this expression. \(lim_{y \to 0}{\frac{\sin 3y}{7y}}\)
Again we will use the theorem \(lim_{\theta \to 0} \frac{\sin \theta}{\theta} = 1 \)
To get the form that we want so we can solve easily we need to multiply the numerator and denominator by \(\frac{3}{7}\).
Once you see how everything cancels out you will see that your answer is also \(\frac{3}{7}\).
Problem 5.
Use the relation \(lim_{\theta \to 0} \frac{\sin \theta}{\theta} =1 \) for the following one-sided limits problem.
\( f(x) = \frac{2x + 2x\cos(2x)}{\sin(2x)\cos(2x)} \) as x approaches 0.
We should write this expression as the sum of two terms.
\(\frac{2x}{\sin(2x)\cos(2x)} + {2x}{\sin(2x)}\)
Now rewrite the first fraction as the product of two fractions and then factor the result.
\(\frac{2x}{\sin(2x)} * \frac{1}{\cos(2x)} + \frac{2x}{\sin(2x)}\)
\(= \frac{2x}{\sin(2x)} \left(\frac{1}{\cos(2x)} + 1\right) \)
Multiply this out and then simplify. I did not show all the Algebra steps there because it is a pain but if you are in calculus this should be trivial for you.
You will this expression: \(\frac{1}{1} \left(\frac{1}{1} +1\right)\)
\(=2\)
Problem 6.
Use the relation \(lim_{\theta \to 0} \frac{\sin \theta}{\theta} =1\) to find out the limit of the function below.
\(f(\theta)=\frac{\sin \theta}{\sin (2\theta)}\)
Multiply \(\frac{\sin \theta}{\sin (2\theta)} by \frac{2\theta}{2\theta} \).
This equals : \(\frac{1}{2} * \frac{\sin \theta}{\theta} * \frac{2\theta}{\sin (2\theta)}\).
We now have: \(\frac{1}{2} * 1 * \frac{1}{1} \).
So you should get \(\frac{1}{2}\) as your answer.
Conclusion
After doing a few problems you should be able to see how useful one-sided limits can be to you. This will be one of your premier tools later on to help you solve problems. Limits often exhibit some wild behavior. That is why we must look at both sides of any particular limit. Sometimes they may be exactly equal on both sides but many times they will not be. Graphing will help when it gets more complicated so I will be using more graphs as we progress.
I hope you enjoyed this article and that it will help your understanding and appreciation of Calculus.
If you are already not a member of my site then please subscribe. I would appreciate it very much!